Pythagorean Theorem Drawing
Pythagorean Theorem Drawing - Side c c is known as the hypotenuse. And this will be true: Sal introduces the famous and super important pythagorean theorem! That means we can draw squares on each side: 1 + 1 = c2. Put in what we know: A 2 + b 2 = c 2. You might recognize this theorem in the form of the pythagorean equation: Discover how to find the length of an edge in a 3d shape using the pythagorean theorem! Thus, for the sides of the triangle in figure 4.4.1, a2 + b2 = c2. That means we can draw squares on each side: The hypotenuse of the right triangle is the side opposite the right angle, and is the longest side. 1 + 1 = c2. Side c c is known as the hypotenuse. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. You can learn more about the pythagorean theorem and review its algebraic proof. The pythagorean theorem states that the sum of squares of the two legs of a right triangle is equal to the square of the hypotenuse, so we need to prove a2 + b2 = c2. This video explains and demonstrates how to begin drawing a pythagorean theorem. That is, leg2 + leg2 = hypotenuse2. Use the distance formula to determine the distance between two points on the coordinate plane. A 2 + b 2 = c 2. If i have 16+64=c2 or squared how do i square root it? This collection offers 4 different approaches for discovering the ins and outs of the pythagorean theorem. And this will be true: Put in what we know: This collection offers 4 different approaches for discovering the ins and outs of the pythagorean theorem. I mean square root 80. Web in mathematics, the pythagorean theorem or pythagoras' theorem is a fundamental relation in euclidean geometry between the three sides of a right triangle. Even the ancients knew of this relationship. The pythagorean theorem states that the sum of squares of the two legs of a right triangle is equal to the square of the hypotenuse, so we need to prove a2 + b2 = c2. Draw a line through vertex c that is perpendicular to the segment ab. In a right triangle with. Congruent triangles are ones that have three identical sides. Web this pythagorean theorem calculator will calculate the length of any of the missing sides of a right triangle, provided you know the lengths of its other two sides. Bhaskara uses a square and four congruent right triangles, rearranged in two ways, to prove this theorem. Web the pythagorean theorem states. And in this day and age of interactivity or press of a button knowledge (aka: Draw four congruent right triangles. In this topic, we’ll figure out how to use the pythagorean theorem and prove why it works. This includes calculating the hypotenuse. Even the ancients knew of this relationship. Web the pythagorean theorem states that the sum of the squared sides of a right triangle equals the length of the hypotenuse squared. A2 + b2 = c2 a 2 + b 2 = c 2. Draw a right triangle, and label the vertices a, b, and c, where c is the vertex of the right angle. Web the pythagorean. This collection offers 4 different approaches for discovering the ins and outs of the pythagorean theorem. Use the pythagorean theorem to determine the length of one side of a right triangle. The hypotenuse of the right triangle is the side opposite the right angle, and is the longest side. Web this pythagorean theorem calculator will calculate the length of any. A + b = c. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. It works the other way around, too: Sal introduces the famous and super important pythagorean theorem! Here, the hypotenuse is the longest side, as it is opposite to the angle 90°. The hypotenuse is the longest side, opposite the right angle. The hypotenuse of the right triangle is the side opposite the right angle, and is the longest side. The pythagorean theorem describes a special relationship between the sides of a right triangle. Want to join the conversation? Web this video explains and demonstrates how to begin drawing a pythagorean theorem spiral diagram. Draw a line through vertex c that is perpendicular to the segment ab. Square root of both sides: 1 + 1 = c2. Pythagorean theorem formula shown with triangle abc abc is: And this will be true: Side c c is known as the hypotenuse. Web this pythagorean theorem calculator will calculate the length of any of the missing sides of a right triangle, provided you know the lengths of its other two sides. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. Given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a+b a+b as shown below: Bhaskara uses a square and four congruent right triangles, rearranged in two ways, to prove this theorem. A 2 + b 2 = c 2.
Pythagoras Theorem explained on a chalkboard Stock Photo Alamy

Pythagoras Theorem Problems, Examples & Formula

Spiral of Pythagoras year 4 Math art projects, Math art, Spiral drawing

Pythagorean theorem, original drawing on prepared paper Pythagorean
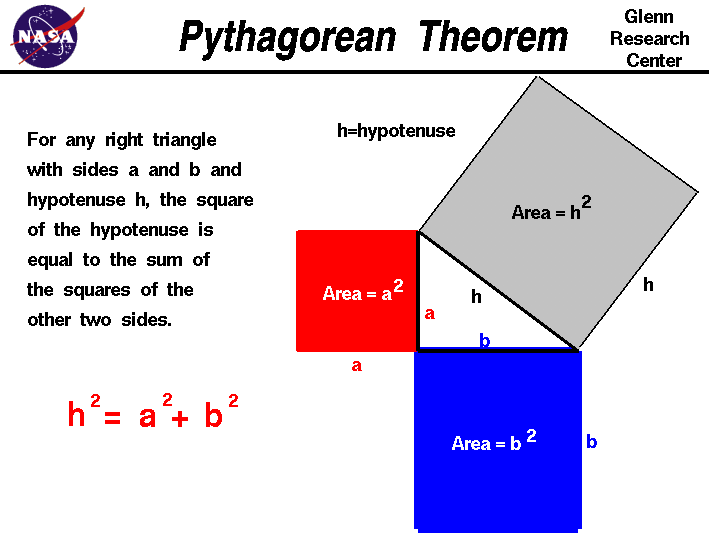
Pythagorean Theorem
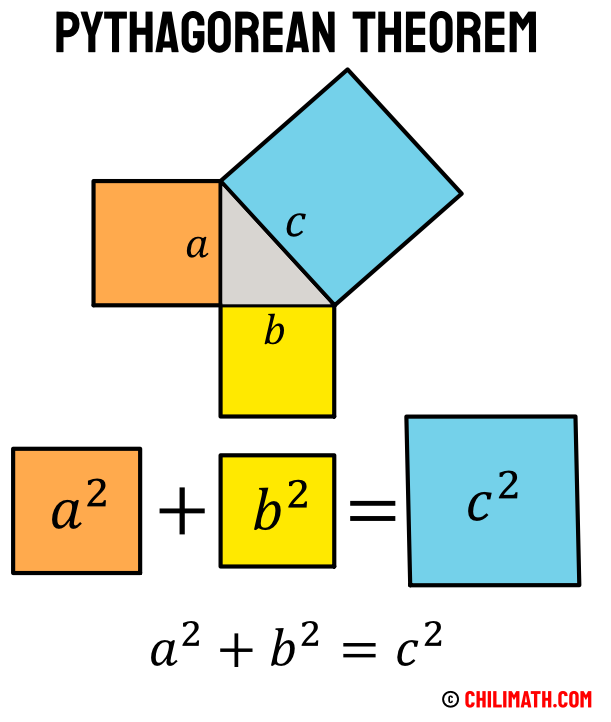
Pythagorean Theorem Definition, Formula & Examples ChiliMath

Pythagorean Theorem Spiral Project A Fun And Educational Activity For

How to Prove the Pythagorean Theorem 10 Steps (with Pictures)
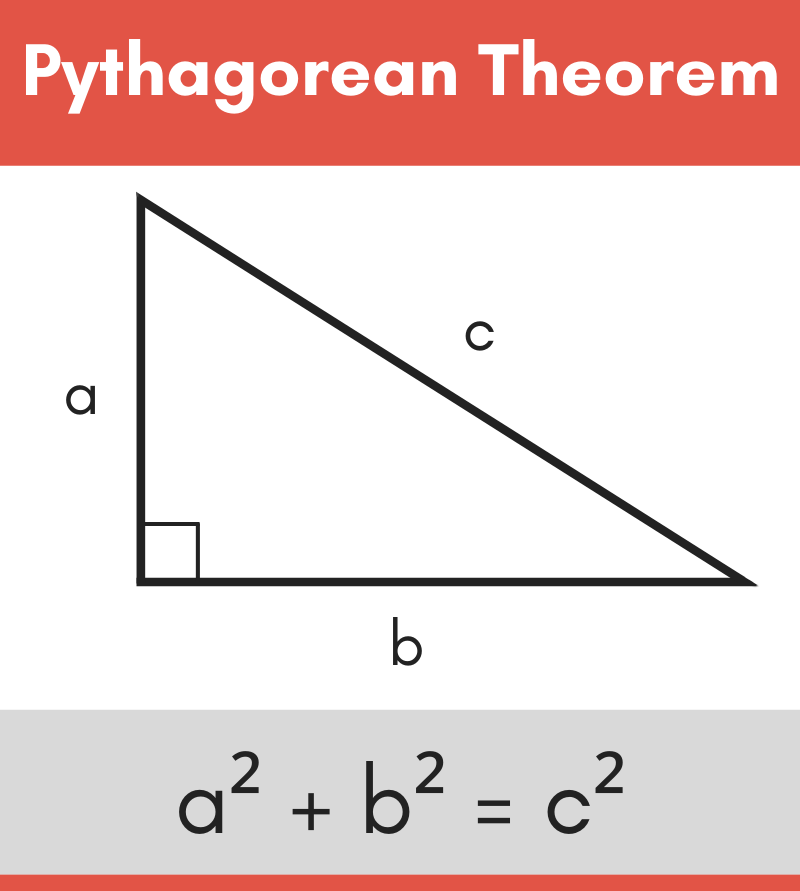
An Introduction To Pythagoras Theorem SyedLearns

pythagorean theorem art Google Search Math art projects, Spiral art
Use The Distance Formula To Determine The Distance Between Two Points On The Coordinate Plane.
6.4K Views 1 Year Ago Mona Shores Middle School.
This Video Explains And Demonstrates How To Begin Drawing A Pythagorean Theorem Tree.
If We Have A Right Triangle, And We Construct Squares Using The Edges Or Sides Of The Right Triangle (Gray Triangle In The Middle), The Area Of The Largest Square Built On The Hypotenuse (The Longest Side) Is Equal To The Sum Of The Areas Of The Squares Built On The Other Two Sides.
Related Post: